Lecture 1 : intro and Word Vectors

---

TL;DR

• Different ways words are represented by computers
  • WordNet : manual labeling, traditional method
  • WordVectors
    • One-Hot Vectors
    • Word Vectors

---

Meaning of a Word

How can we represent the meaning of a word?

Wordnet

Previously utilized NLP solution : WordNet

Discrete Symbols

• Representing words as discrete symbols as one-hot-vectors
• Problem
  • If a user searches for “Seattle motel”, we would like to matchdocuments containing “Seattle hotel”.
  • However, the two vectors below are orthogonal, so there is no similarity between the two in one-hot-vectors

motel = [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]
hotel = [0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]

• Solution
  • Could try to rely on WordNet’s list of synonyms to get similarity?
    • But it is well-known to fail badly: incompleteness, etc.
  • Instead: learn to encode similarity in the vectors themselves

WordNet

• Wordnet is a lexical database of semantic relations between words in English first created by CogSys Lab of Princeton University.
• It includes N, V, ADJ, ADV but omits PREP, DET, and other function words.
• WordVec for other langauges exists too.

WordNet Example

Downloading nltk and wordnet

import nltk
nltk.download('wordnet')

from nltk.corpus import wordnet as wn

print('Synsets for the word "invite" in WordNet:\n\n', wn.synsets('invite'))

Synsets for the word "invite" in WordNet:

 [Synset('invite.n.01'), Synset('invite.v.01'), Synset('invite.v.02'), Synset('tempt.v.03'), Synset('invite.v.04'), Synset('invite.v.05'), Synset('invite.v.06'), Synset('invite.v.07'), Synset('receive.v.05')]

# We can constrain the search by specifying the part of speech
# parts of speech available: ADJ, ADV, ADJ_SAT, NOUN, VERB
# ADJ_SAT: see https://stackoverflow.com/questions/18817396/what-part-of-speech-does-s-stand-for-in-wordnet-synsets

# Way one
print(f'{"-"*20}Way one{"-"*20}')
print('Synsets for the noun "invite" in WordNet:\n\n', wn.synsets('invite', pos=wn.NOUN))

# Way two
print(f'\n\n{"-"*20}Way two{"-"*20}')
# pos: {'n':'noun', 'v':'verb', 's':'adj (s)', 'a':'adj', 'r':'adv'}
print('Synsets for the noun "invite" in WordNet:\n\n', [s for s in wn.synsets('invite') if s.pos()=='n'])

--------------------Way one--------------------
Synsets for the noun "invite" in WordNet:

 [Synset('invite.n.01')]


--------------------Way two--------------------
Synsets for the noun "invite" in WordNet:

 [Synset('invite.n.01')]

# check definition of a synset
print(f'{"-"*20}Definition{"-"*20}')
print('The definition for invite as a noun:\n\n', wn.synset('invite.n.01').definition())

# check the related examples
print(f'\n\n{"-"*20}Examples{"-"*20}')
print('The definition for invite as a noun:\n\n', wn.synset('invite.n.01').examples())

# check the hypernyms
print(f'\n\n{"-"*20}Hypernyms{"-"*20}')
print('The hypernyms for invite as a noun:\n\n', wn.synset('invite.n.01').hypernyms())

--------------------Definition--------------------
The definition for invite as a noun:

 a colloquial expression for invitation


--------------------Examples--------------------
The definition for invite as a noun:

 ["he didn't get no invite to the party"]


--------------------Hypernyms--------------------
The hypernyms for invite as a noun:

 [Synset('invitation.n.01')]

Limitations

• Requires human labor
  • Impossible to update every word
• Missing nuance
  • "proficient" is listed as a synoynm for "good"
• Misses new words
  • badass, nifty, etc
• Cannot compute word similarity accurately (score range : 0~1)

dog = wn.synset('dog.n.01')
cat = wn.synset('cat.n.01')
print('The path similarity between cat(noun) and dog(noun): ', dog.path_similarity(cat))

The path similarity between cat(noun) and dog(noun):  0.2

Word Vectors(AKA Embeddings)

• When a word w appears in a text, the context is the set of words that appear nearby.
• Context words build up a representation of w
• A dense vector for each word is created, measuring similarity as the vector dot product

Word Space

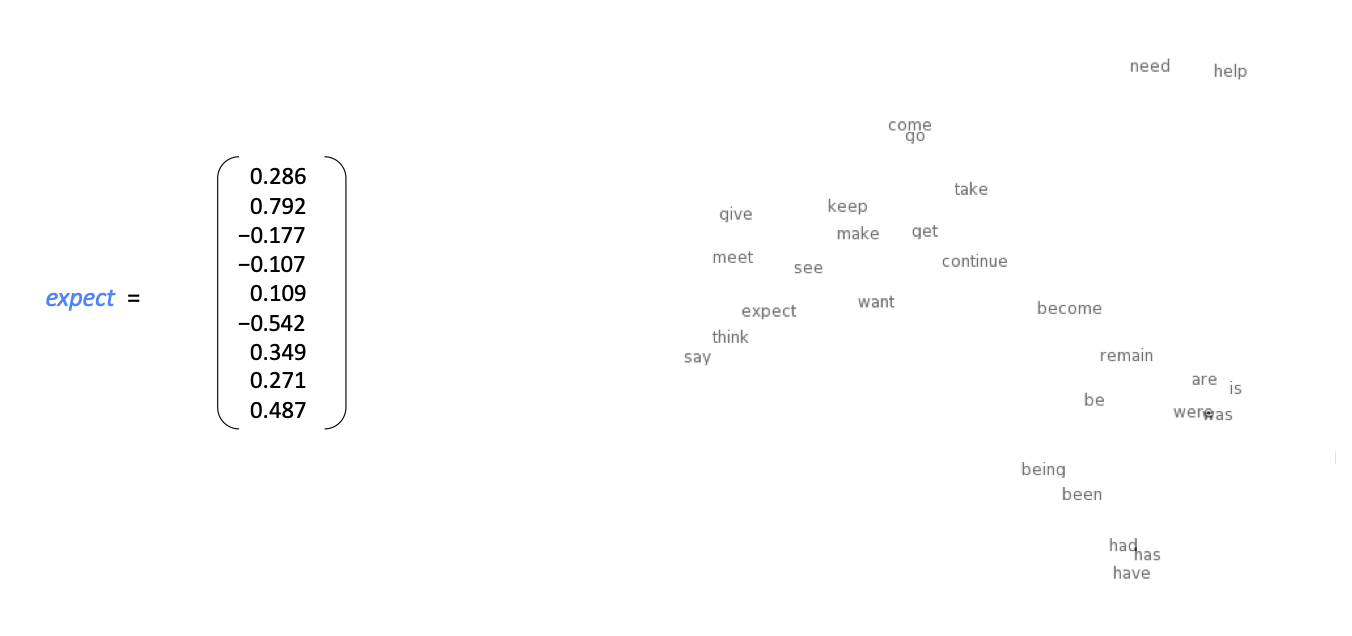
• note that:
  • has, have, had are grouped together
  • come, go are closely groupd

Word2vec

Word2Vec is a frameword for learning word vectors

How it works:

1. Get a large corpus(latin word for body) of text
2. Create a vector for each word in a fixed vocabulary
3. Go through each position t in the text, which has center word c and context words o
4. Find the probability of o given c(or vice versa) using the similarity of word vectors for c and o
5. Keep adjusting this

core idea : What is the probability of a word occuring in the context of the center word?

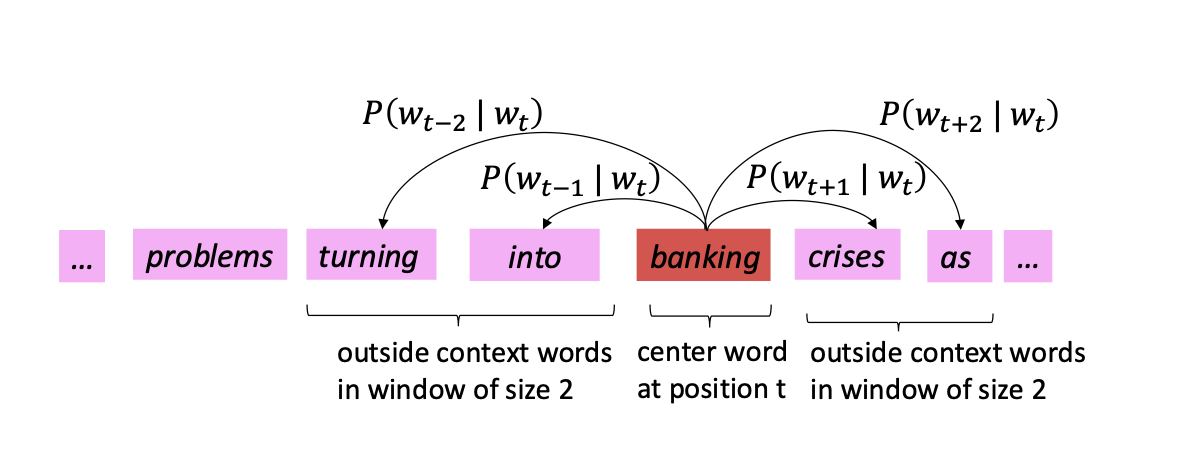
If the window = 2, then it predicts the likelihood of the 2 words that come before and after the center word.

Objective Function

Likelihood : measure of how "fit" a given data sample is to a model. For each position t = 1, ..., T, predict context words within a window of fixed size m, given center word w_j.

Data Likelihood Formula :

$$ Likelihood = L(\theta) = \prod_{t=1}^{T} \prod_{\substack{-m \leq j \leq m \\ j \neq 0}} P(w_{t+j} \mid w_t; \theta) $$

# Likelihood Function 

import numpy as np

def likelihood(X, theta):
    """
    Computes the likelihood function for given data X and parameter theta.
    Assumes a Gaussian likelihood with mean=theta and variance=1.
    """
    return np.prod(1 / np.sqrt(2 * np.pi) * np.exp(-0.5 * (X - theta)**2))

# Example Usage
np.random.seed(42)
X = np.random.normal(loc=5, scale=2, size=100)  # Sample data from Gaussian

theta_test = 5.0
likelihood_val = likelihood(X, theta_test)
print("Likelihood:", likelihood_val)

Likelihood: 1.7064553444710973e-112

Objective Function(AKA : loss function) : this is what is to be minimized. Low loss means greater accuracy.

Loss Function Formula:

$$ J(\theta) = -\frac{1}{T} \log L(\theta) = -\frac{1}{T} \sum_{t=1}^{T} \sum_{\substack{-m \leq j \leq m \\ j \neq 0}} \log P(w_{t+j} \mid w_t; \theta) $$

• This is the average negative log likelihood

Next question : How is P(probability) calculated? -> prediction function

# Negative Log-Likelihood Function
def negative_log_likelihood(X, theta):
    """
    Computes the Negative Log-Likelihood (NLL) for a Gaussian distribution.
    """
    return -np.sum(-0.5 * (X - theta)**2 - 0.5 * np.log(2 * np.pi))

nll_val = negative_log_likelihood(X, theta_test)
print("Negative Log-Likelihood:", nll_val)

Negative Log-Likelihood: 257.3551120942153

Prediction function

For a given center word c the probability of a context word o appearing is:

$$ P(o \mid c) = \frac{\exp(u_o^T v_c)}{\sum_{w \in V} \exp(u_w^T v_c)} $$

Numerator

$$ \exp(u_o^T v_c) $$

• Calculates the similarity between target and context word
• $ u_o^T v_c $ is the dot product between vector representations of o and c -> measure of how similar the two words are in embedding space
• Applying the exponential function (exp) ensures that the result is always positive and helps in normalizing the values.

Denominator

$$ \sum_{w \in V} \exp(u_w^T v_c) $$

• Calculates sum over all possible words
• Ensures that the probability values sum to 1, making the formula a valid probability distribution

Softmax function

• TLDR: The softmax function converts a vector of real numbers into a probability distribution
• Why use this?
  • The output values lie in the range of (0,1) and sum to 1, making them interpretable as probabilities.
  • In the final layer of a NN, softmax ensures that predictions are probabilities over multiple classes.
• "max" because amplifies probability of largest $ x_i $
• "soft" because still assigns some probability to smaller $ x_i $

$$ \text{softmax}(x_i) = \frac{\exp(x_i)}{\sum_{j=1}^{n} \exp(x_j)} $$

# Prediction Function
def softmax(x):
    """
    Computes the softmax function for an array x.
    """
    exp_x = np.exp(x - np.max(x))  # For numerical stability
    return exp_x / exp_x.sum()

def predict_probabilities(word_vector, context_vector, vocabulary):
    """
    Computes P(o|c) using softmax, given word embeddings.
    """
    scores = np.dot(vocabulary, context_vector)  # Dot product with all words
    return softmax(scores)


# Prediction Example
vocab_size = 10
embedding_dim = 5
vocabulary = np.random.rand(vocab_size, embedding_dim)  # Fake word embeddings
context_vector = np.random.rand(embedding_dim)
probabilities = predict_probabilities(vocabulary, context_vector, vocabulary)
print("Prediction Probabilities:", probabilities)

Prediction Probabilities: [0.07444069 0.13176847 0.10419385 0.06380236 0.10424873 0.11576871
 0.11774626 0.06498345 0.09594868 0.12709881]

Optimization

Training the model :